数据结构与算法
数据结构与算法的概述
数据结构与算法的介绍
算法
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
算法是独立存在的一种解决问题的方法和思想。
- 对于算法而言,实现的语言并不重要,重要的是思想。
算法可以有不同的语言描述实现版本(如C描述、C++描述、Python描述等)
案列一
- 有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。
案列二
- 有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第4个月后,每个月又生一对兔子,假如兔子不死,问每个月的兔子总数为多少?
数据结构
- 数据结构就是把数据组织起来,为了更方便地使用数据我们为了解决问题,需要将数据保存下来,然后根据数据的存储方式来设计算法实现进行处理,那么数据的存储方式不同就会导致需要不同的算法进行处理。我们希望算法解决问题的效率越快越好,于是我们就需要考虑数据究竟如何保存的问题,这就是数据结构。
- 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
数据结构与算法关系
- 程序 = 数据结构 + 算法
- 数据结构是算法的基础。
- 图书馆储藏书籍你肯定见过吧?为了方便查找,图书管理员一般会将书籍分门别类进行“存储”。按照一定规律编号,就是书籍这种“数据”的存储结构。
- 那我们如何来查找一本书呢?有很多种办法,你当然可以一本一本地找,也可以先根据书籍类别的编号,是人文,还是科学、计算机,来定位书架,然后再依次查找。笼统地说,这些查找方法都是算法。
- 数据结构和算法是相辅相成的。数据结构是为算法服务的,算法要作用在特定的数据结构之上。 因此,我们无法孤立数据结构来讲算法,也无法孤立算法来讲数据结构。
线性结构和非线性结构
线性结构
- 线性结构作为最常用的数据结构,其特点是数据元素之间存在一对一的线性关系。
- 线性结构有两种不同的存储结构,即顺序存储结构(数组)和链式存储结构(链表)。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的。
- 链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素结点存放数据元素以及相邻元素的地址信息。
- 线性结构常见的有:数组、队列、链表和栈。

非线性结构
二维数组、多维数组、广义表、树结构、图结构
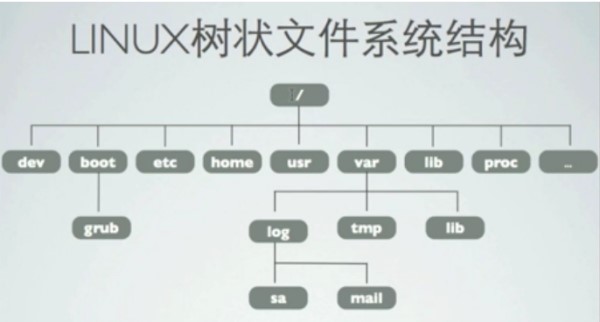
栈
栈的介绍
栈是限制插入和删除只能在一个位置上进行的线性表。
其中,允许插入和删除的一端位于表的末端,叫做栈顶(top),不允许插入和删除的另一端叫做栈底(bottom)。对栈的基本操作有 PUSH(压栈)和 POP (出栈),前者相当于表的插入操作(向栈顶插入一个元素),后者则是删除操作(删除一个栈顶元素)。栈是一种后进先出(LIFO)**的数据结构,最先被删除的是最近压栈的元素。
栈的结构图
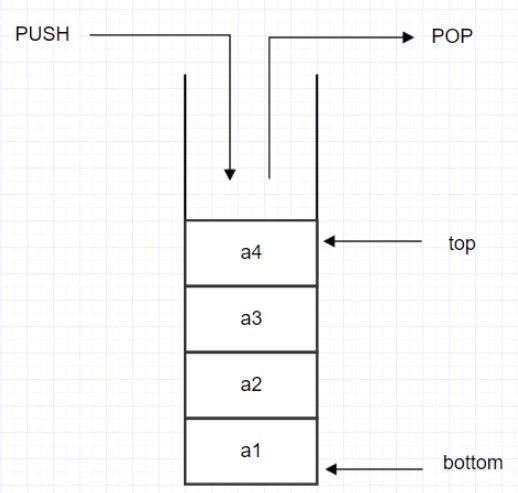
压栈图
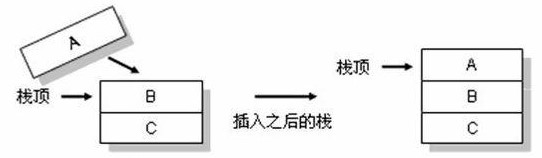
弹栈图
栈实现
- 由于栈是一个表,因此任何实现表的方法都可以用来实现栈。主要有两种方式,链表实现和数组实现。
链表实现块
- 可以使用单链表来实现栈。通过在表顶端插入一个元素来实现 PUSH,通过删除表顶端元素来实现 POP。使用链表方式实现的栈又叫动态栈。动态栈有链表的部分特性,即元素与元素之间在物理存储上可以不连续,但是功能有些受限制,动态栈只能在栈顶处进行插入和删除操作,不能在栈尾或栈中间进行插入和删除操作
数组实现块
- 栈也可以用数组来实现。使用数组方式实现的栈叫静态栈。
栈的应用场景
- 子程序的调用,在跳往子程序前,会将下一个指令的地址存到堆栈中,知道子程序执行完后再将地址取出,以回到原来的程序中。
- 处理递归调用:和子程序的调用类似,只是除了存储下一个指令的地址外,也将参数,区域变量等数据存入堆栈中。
- 表达式的转换:【中缀表达式转后缀表达式】与求值()实际解决
栈的快速入门
练习:使用数组来模拟栈
public class ArrayStack {
//定义栈的大小
private int maxStack;
//定义一个数组来模拟栈
private int[] stack;
//栈帧所在的位置,默认情况下没有数据返回-1
private int top = -1;
//使用构造函数初始化栈的大小
public ArrayStack(int maxStack) {
this.maxStack = maxStack;
stack = new int[maxStack];
}
/**
* 压栈
* 弹栈
* 判断栈中是否为空
* 判断栈中是否已满
*/
/**
* 先判断是否为空栈
*/
public boolean isNull(){
return this.top == -1;
}
/**
* 判断是否为满栈
*/
public boolean isFull(){
return this.top == stack.length-1;
}
/**
* 压栈
*/
public void posh(int i){
//先判断栈是否满栈,若满栈则抛出异常
if (isFull()){
throw new RuntimeException("栈已满!!");
}
stack[++top] = i;
}
/**
* 弹栈
*/
public int pop(){
//先判断栈是否为空
if (isNull()){
throw new RuntimeException("栈已空!!");
}
int value = stack[top--];
return value;
}
/**
* 查看栈中所有的元素
*/
public void list(){
if (isNull()){
throw new RuntimeException("空栈,没有找到数据");
}
for (int i : stack) {
System.out.println(i);
}
}
/**
* 栈中元素的个数
*/
public int length(){
return this.top+1;
}
}
测试:使用模拟的栈来测试一个字符串是否是回文数据。
- 回文数据:就是压栈前,与弹栈后的字符串相同
- 例如:aba , abcba就是回文数据
public class TestApp {
public static void main(String[] args) {
/**
* 回文数据
* 回文:aba abcdcba
* 回文就是正反过来数据不会变
* 下面,由模拟的栈来判断一个字符串是否是回文数据
*/
boolean abc = method("aba");
System.out.println(abc);
}
//定义方法,调用栈来测试字符串是否为回文数据
public static boolean method(String s){
/**
* 初始化栈对象
*/
ArrayStack arrayStack = new ArrayStack(10);
/**
* 获取字符串
* 将字符串压入栈中
*/
for (int i = 0; i < s.length(); i++) {
arrayStack.posh(s.charAt(i));
}
/**
* 获取栈中的数据
*/
//定义一个字符串
String s1 = "";
int length = arrayStack.length();
for (int i = 0; i < length; i++) {
if (arrayStack.isNull()){
throw new RuntimeException("空栈");
}
char pop = (char)arrayStack.pop();
s1 += pop;
}
return s.equals(s1);
}
}
链表
链表(Linked List)介绍
算法
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
算法是独立存在的一种解决问题的方法和思想。
- 对于算法而言,实现的语言并不重要,重要的是思想。
算法可以有不同的语言描述实现版本(如C描述、C++描述、Python描述等)
案列一
- 有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。
案列二
- 有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第4个月后,每个月又生一对兔子,假如兔子不死,问每个月的兔子总数为多少?
数据结构
- 数据结构就是把数据组织起来,为了更方便地使用数据我们为了解决问题,需要将数据保存下来,然后根据数据的存储方式来设计算法实现进行处理,那么数据的存储方式不同就会导致需要不同的算法进行处理。我们希望算法解决问题的效率越快越好,于是我们就需要考虑数据究竟如何保存的问题,这就是数据结构。
- 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
线性结构
- 线性结构作为最常用的数据结构,其特点是数据元素之间存在一对一的线性关系。
- 线性结构有两种不同的存储结构,即顺序存储结构(数组)和链式存储结构(链表)。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的。
- 链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素结点存放数据元素以及相邻元素的地址信息。
- 线性结构常见的有:数组、队列、链表和栈。

非线性结构
二维数组、多维数组、广义表、树结构、图结构

栈是限制插入和删除只能在一个位置上进行的线性表。
其中,允许插入和删除的一端位于表的末端,叫做栈顶(top),不允许插入和删除的另一端叫做栈底(bottom)。对栈的基本操作有 PUSH(压栈)和 POP (出栈),前者相当于表的插入操作(向栈顶插入一个元素),后者则是删除操作(删除一个栈顶元素)。栈是一种后进先出(LIFO)**的数据结构,最先被删除的是最近压栈的元素。
栈的结构图

压栈图

弹栈图

栈实现
- 由于栈是一个表,因此任何实现表的方法都可以用来实现栈。主要有两种方式,链表实现和数组实现。
链表实现块
- 可以使用单链表来实现栈。通过在表顶端插入一个元素来实现 PUSH,通过删除表顶端元素来实现 POP。使用链表方式实现的栈又叫动态栈。动态栈有链表的部分特性,即元素与元素之间在物理存储上可以不连续,但是功能有些受限制,动态栈只能在栈顶处进行插入和删除操作,不能在栈尾或栈中间进行插入和删除操作
数组实现块
- 栈也可以用数组来实现。使用数组方式实现的栈叫静态栈。
练习:使用数组来模拟栈
public class ArrayStack {
//定义栈的大小
private int maxStack;
//定义一个数组来模拟栈
private int[] stack;
//栈帧所在的位置,默认情况下没有数据返回-1
private int top = -1;
//使用构造函数初始化栈的大小
public ArrayStack(int maxStack) {
this.maxStack = maxStack;
stack = new int[maxStack];
}
/**
* 压栈
* 弹栈
* 判断栈中是否为空
* 判断栈中是否已满
*/
/**
* 先判断是否为空栈
*/
public boolean isNull(){
return this.top == -1;
}
/**
* 判断是否为满栈
*/
public boolean isFull(){
return this.top == stack.length-1;
}
/**
* 压栈
*/
public void posh(int i){
//先判断栈是否满栈,若满栈则抛出异常
if (isFull()){
throw new RuntimeException("栈已满!!");
}
stack[++top] = i;
}
/**
* 弹栈
*/
public int pop(){
//先判断栈是否为空
if (isNull()){
throw new RuntimeException("栈已空!!");
}
int value = stack[top--];
return value;
}
/**
* 查看栈中所有的元素
*/
public void list(){
if (isNull()){
throw new RuntimeException("空栈,没有找到数据");
}
for (int i : stack) {
System.out.println(i);
}
}
/**
* 栈中元素的个数
*/
public int length(){
return this.top+1;
}
}
测试:使用模拟的栈来测试一个字符串是否是回文数据。
- 回文数据:就是压栈前,与弹栈后的字符串相同
- 例如:aba , abcba就是回文数据
public class TestApp {
public static void main(String[] args) {
/**
* 回文数据
* 回文:aba abcdcba
* 回文就是正反过来数据不会变
* 下面,由模拟的栈来判断一个字符串是否是回文数据
*/
boolean abc = method("aba");
System.out.println(abc);
}
//定义方法,调用栈来测试字符串是否为回文数据
public static boolean method(String s){
/**
* 初始化栈对象
*/
ArrayStack arrayStack = new ArrayStack(10);
/**
* 获取字符串
* 将字符串压入栈中
*/
for (int i = 0; i < s.length(); i++) {
arrayStack.posh(s.charAt(i));
}
/**
* 获取栈中的数据
*/
//定义一个字符串
String s1 = "";
int length = arrayStack.length();
for (int i = 0; i < length; i++) {
if (arrayStack.isNull()){
throw new RuntimeException("空栈");
}
char pop = (char)arrayStack.pop();
s1 += pop;
}
return s.equals(s1);
}
}
-



